"Чем меньше задачи в плане, тем точнее оценки и, следовательно, точнее план".
Короткий ответ - это неверно.
Длинный ответ - верное обратное.
Пусть вам надо сделать одно дело, которое можно разбить на два дела поменьше X и Y. Сколько времени займет каждое дело X и Y мы знаем только примерно.
Дальше верно два утверждения, которые можно проверить в любом учебнике вероятности на свой вкус.
- Мат ожидание суммы равно сумме мат ожиданий
- Дисперсия суммы - это сумма дисперсий и двух ковариаций
Если два дела X и Y независимы, то ковариация равна нулю. Мы получаем, что разбив задачу на две, мы получили неопределенность конечного результата как сумму неопределенностей.
Загадочная ковариация входит в игру, если есть жесткая зависимость хотя бы между последовательностью их выполнения (если это задача с чайником где надо налить воду и включить чайник) или еще хуже результат одной задачи, частично используется в другой.
Давайте, посчитаем сценарий
- Х - нормально распределенная случайная величина N(10, 3)
- Y = max(X, N(10, 3)) - второй шаг априорно оценивается так же, но если первый шаг будет чуть больше (10.5), то второй займет столько же как и первый.
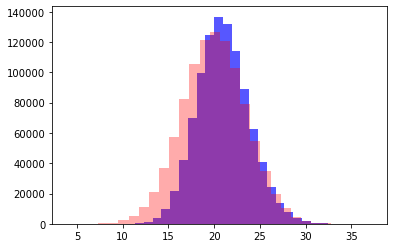
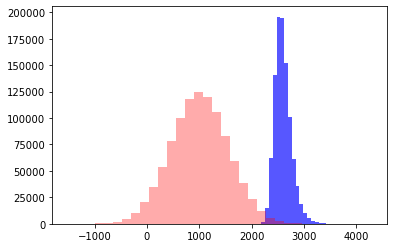
Получим примерно такую картину (красное сумма двух независимых N(10, 3), синее - X+Y)
- Дисперсия "по плану" = 3+3=6, Дисперсия "по факту" = 8.1
- Среднее "по плану" = 10 + 10 = 20, Среднее "по факту" = 20.98
- Распределение поехало вправо
Давайте попробуем с расширить пример до 5 задач.
Те же условия, "сложность" накапливается с каждым шагом
- Х = N(10, 3)
- Y = max(X, N(10, 3))
- A = max(Y, N(10, 3))
- B = max(A, N(10, 3))
- C = max(B, N(10, 3))
Численный эксперимент
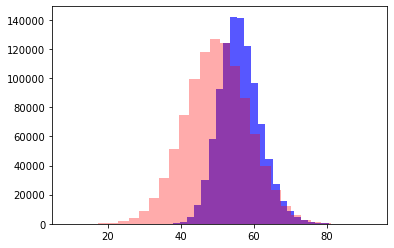
- Дисперсия: 15 vs 30.97
- Среднее: 50 vs 56.23
- Распределение поехало вправо сильнее
Иллюстрация о "пользе" дробления на мелкие задачи в данном сценарии - один и тот же объем работы разделим на 10, 100 и 1000 задач
N = 10. Самый короткий план, и самый точный
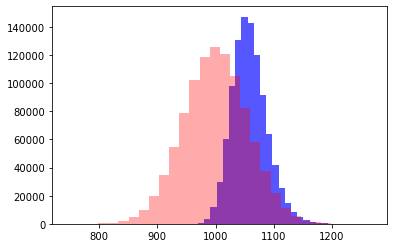
N = 100
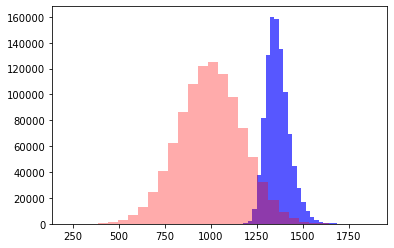
N = 1000. Самый детальный план, и самый ошибочный
Чем более шагов у вас в плане, тем он более неточный.
Может вы имеете дело с загадочной проблемой, а может метод вносит системную ошибку.
Можно сказать что это такой выдуманный пример, но это лишь иллюстрация формулы из любого учебника теории вероятности.
Встретите зависимые задачи - вспомните про ковариации и добавьте к итоговой оценке. Два раза.
Вот тут неадо немного аккуратнее быть. Что такое неопределенность? У нас нет такого понятия :-) Мы же пока только дисперсиями оперируем.
А дисперсия - это хитрая такая мера разброса - это же сумма квадратов отклонений от матожидания. И эта квадратичная зависимость дальше может внести свою лепту.
Если мы под неопределенностью будем рассматривать среднее отклонение (а не среднеквадратичное, которое является корнем из дисперсии), то там появится нелинейность. В данном случае - сумма неопределенностей будет меньше, чем неопределенность суммы :-)
Тут немного смысл не понял... Это у нас длительность отдельной задачи? То есть, длительность Y не модет быть меньше длительности X? Как это связано с чайником? И какому явлению в реальной жизни может соответствовать такая модель? Не догнал я тут немного...
Кстати, отдельной статьи достойна идея про ненормальные распределения. Как только там появляется не симметрия (как у логнормального, например), то тут же идет дополнительные чудеса...
Вспомнил какой-то свой древний доклад еще начала 00х:
"Сколько времени займет каждое дело X и Y мы только примерно."
У вас тут дезиртировало какое то слово.
"Мат ожидание суммы равно сумме мат ожиданий
Дисперсия суммы - это сумма дисперсий и двух ковариаций"
(тут бы еще определение плотности вероятности поднять и можно тушить свет)
Это наверное да, но ...
Кажется вы запутали себя и окружающих сложной терминологией.
Хочу привести очень простой контрпример.
Предположим оба под-дела независимы и если спросить меня сколько они займут я скажу "от 1 до 6 часов, и я ничего не знаю про распределение этих вероятностей".
Тогда уместная модель будет сказать что это 1d6 часов на каждую подзадачу.
А если спросить меня про дело в целом я скажу "от 2 до 12 часов, и я ничего не знаю про распределение этих вероятностей". То есть я бы мог порассуждать про подзадачи и понять что, что-то знаю, но я этого не делал и не знаю.
Тогда уместная модель будет сказать что это 1d11 + 1 часов на каждую подзадачу.
В первом случае вероятность исходов 2 и 12 = 1/36 а вероятность исхода 7 = 1/6.
Во втором же все 3 исхода имеют вероятность 1/11. (дробные длительности для простоты игнорируем).
Сдается мне в первом случае дисперсия таки меньше. Ну и очевидно эта оценка дает больше ценной информации.
Особенно если исключить вероятность того что на самом деле есть еще под-задача Z которую мы просто не видели :-) А она там обычно есть, и не вероятность а задача.
Очень хорошая статья про неопределенность от Эли Шрегенхайма: https://elischragenheim.com/2023/11/18/fighting-uncertainty-as-a-critical-part-in-managing-organizations/
(ее перевод)